How to Fix Error Propagation Calculation [+Quick Solutions]

Introduction: Error propagation calculations are an essential part of any scientific experiment. It involves analyzing how errors in measured quantities affect the final result. However, errors can propagate and accumulate, leading to inaccurate results. In this article, we will discuss how to fix propagation calculation errors and ensure accurate results.

How to Fix Error Propagation Calculation

However, it is prone to errors that can skew the results. To fix error propagation calculations and ensure accurate results, you need to understand the sources of error, use the correct formulas, and check your calculations. This comprehensive guide will teach you how to fix error propagation calculations, avoid common mistakes, and achieve accurate results.

At first

When performing calculations such as processing experimental results, errors often have to be considered.

The error of the function value calculated using the value containing the error is

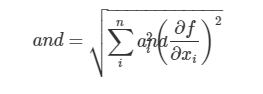
(We will not derive this equation here). As you can see, this is cumbersome to calculate.
Even in the division, partial derivative is troublesome, but it would be ridiculous if an exponential function or a logarithmic function appeared.
So I decided to “let Python do the boring stuff.”

Execution environment

• Windows 10
• Python 3.8.3

Since it uses an f-string, it works after 3.6.

Library

I’m using NumPy for the time being, but I don’t actually need it.
, but this is substitutable.
The reason why we took trouble importing it is to be able to use the exponential and logarithmic functions that often appear in scientific calculations.
I think copy is included as standard. NumPy.sqrt**(1/2)

Source Code

import NumPy
from copy import copy
from math import inf

def calc_eps():
a = 4 / 3
b = a - 1
c = b + b + b
return 1 - c

EPS = calc_eps()

def eval_func(func, beta):
if callable(func):
return func(beta)

for i, b in enumerate(beta):
Func = func.replace(f'${{{i+1}}}', str(b))
return eval(func)

def diff(func, beta, index):
last_d = 0.0
d = inf
err = inf
last_e = inf
eps = 1
step = 1.1 # Step for eps
v = eval_func(func, beta)

while abs(last_d - d) > EPS:
if eps <= EPS: break beta2 = copy(beta) beta2[index] += eps tmp = eval_func(func, beta2) - v if tmp == 0.0: break err = abs((last_d - d) / (step - 1)) # Estimate error if err > last_e:
break
last_e = err
last_d = d
d = tmp / eps
eps /= step
return last_d

def parse_data(data, err=None):
beta = [x[0] for x in data] if err is None else data
err = [x[-1] for x in data] if err is None else err
return beta, err

def calc_error(func, beta, err):
E = 0.0
for I, e in enumerate(err):
E += (diff(func, beta, i)2) * (e2)
return NumPy.sqrt(E)

def calc_with_error(func, data, err=None):
beta, err = parse_data(data, err)
return eval_func(func, beta), calc_error(func, beta, err)

def get_digit(value):
return int(numpy.log10(value) // 1)

def separate_exp(value):
d = get_digit(value)
m = value / (10**d)
return m, d

def round at(Val, digit):
d = get_digit(Val)
sign = Val / NumPy.absolute(Val)
coeff = 10 ** (d - digit)
Val /= coeff
Val = int(Val + 0.5 * sgn) * coeff
return value

def format_value(Val, err, show_sign=False):
if Val < 0:
Val = -val
sign = '-'
else:
sign = '' if not show_sign else '+'

s_err, d_err = separate_exp(err)
s_err = int(round(s_err))
if s_err >= 10:
s_err //= 10
d_err += 1
d_val = get_digit(val)

d = d_val - d_err

s_val = roundat(val, d)
m = f'{s_val:e}'.split('e')[0] + '0' * d
width = 1 if d <= 0 else 2 + d
m = m[:width]

err = str(s_err)

if not d_val >= d_err:
d_val = d_err

return f'{sgn}{m}({err})E{d_val}'

def main():
f = '${1} * ${2} / ${3}'
data = [(25.4, 0.5), (1.56, 0.01), (13.5, 0.2)]

value, error = calc_with_error(f, data)

print(value: {value}')
print(f'Error: {error}')
print(format_value(value, error))

if name == 'main':
main()

• Explanation

It’s long and dull, so I’ll fold it.

explanation

Execution example

In 25.4(5)×1.56(1)/13.5(2) shown in the above code,

Value: 2.9351111111111114
Error: 0.07471981498926973
2.94(7)E0

is displayed.

verification

If you actually do your best with hand calculations,

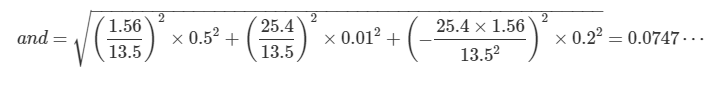
Then, we were able to confirm that the calculation was accurate even in Python.

At last

There are many parts that I manage to do through hard work, so I would appreciate it if you could tell me if there is a better way to write.

FAQs:

Q: What is the difference between systematic and random errors?

A: Systematic errors are caused by flaws in experimental design, while random errors are caused by chance variations.

Q: How do I calculate uncertainties?

A: Uncertainties can be calculated using statistical methods or from the instrument specifications.

Q: What is the error propagation formula?

A: The error propagation formula is a mathematical expression that describes how errors in measured quantities affect the final result.

Q: Can error propagation be avoided?

A: Error propagation cannot be completely avoided, but it can be minimized by using appropriate experimental design, reducing instrument errors, and understanding the sources of error.

Conclusion:

Error propagation calculation are a crucial step in any scientific experiment. It ensures that the final result is accurate and reliable. However, it is prone to errors that can skew the results. To fix Error propagation calculation, you need to understand the sources of errors, use the correct formulas, and check your calculations. By following the tips for accurate error propagation calculations, you can ensure that your results are reliable and trustworthy.