Relative Error Calculator |Relative Error| Bug Free Soft

The relative error can be explained as the uncertainty of the measured value versus the true value. To calculate relative error, we should even calculate the absolute error.

Table of Contents Show

No measurement is error-free, or the probability of error-free measurement approaches zero. The error types and causes of errors are very diverse and influenced by many factors (Figure 1.2)

The general characteristics of the influencing factors can be systematized from various perspectives, for example, under the influence of the listed factors (Figure 1.2).

According to the results of measurements, errors can be divided into three types: systematic, random, and lossy.

Systematic errors, in turn, are divided into groups by the nature of their occurrence and manifestation. These can be eliminated in various ways, for example, by introducing changes.

Pilaf. 1.2

Random errors It is caused by a complex set of changing factors, often unknown and difficult to analyze. Their effect on the measurement result can be reduced by multiple measurements, for example, by further statistical processing of the results obtained by the probability theory method.

Withmissesthe experiment involves significant errors that occur with sudden changes in conditions. These errors are also random and should be eliminated once identified.

The accuracy of measurements is estimated by measurement errors, divided instrumentally and methodically according to the nature of their occurrence, and relative and reduced according to the calculation method.

Instrumental error is characterized by the accuracy class of the measuring device, which is given in its passport in the form of standardized basic and additional errors.

Methodical error is due to the defectiveness of methods and measuring instruments.

The absolute error is the difference between the measured G-u and the actual G-values of the quantity, determined by the formula:

Δ=DG=G u -G

Note that the quantity has the size of the measured amount.

The Relative error calculator is found inequality

δ=±ΔG/G u 100%

the given error is calculated by the formula (accuracy class of the measuring instrument)

δ=±ΔG/G normal 100%

where G norms are the normalization value of the measured quantity. It is taken equal to:

a) if the zero mark is on or off the edge of the scale, the final value of the scale of the device;

(b) if the zero sign is located within the scale, the sum of the final values of the scale, excluding the signs;

c) If the scale is not equal, the length of the scale.

The accuracy class of the device is determined during its verification and is a normalized error calculated by formulas.

100%γ Gm=constant if ±=∆ΔG/G is normal

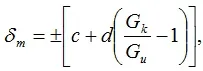
where ΔG m is the most significant possible absolute error of the device;

G k is the final value of the measurement limit of the device; c and d are the coefficients that take into account the design parameters and features of the measuring mechanism of the device.

For example, equality occurs for a voltmeter with a constant relative error.

δm =±c

Relative and reduced errors are associated with the following dependencies:

a) for any value of the reduced error

δ=±γ G norms /G u

b) for the greatest reduced error

δ=±γ m G norms /G u

From these relations, it is concluded that when measuring in a circuit with the same voltage value, for example, with a voltmeter, the relative error is greater, and the measured voltage is lower. And if this voltmeter is chosen incorrectly, the relative error may be proportional to the value.

G n is invalid. Under the terminology of the tasks being solved, for example, when measuring the voltage G \u003d U, when measuring the current C \u003d I, remember that the letter definitions in the formulas for calculating errors should be replaced with the corresponding symbols.

Example 1.1. γ voltmeter with m = 1.0%, U n \u003d G norms, G k \u003d 450 V, measure the voltage U equal to 10 V. Let’s predict measurement errors.

Solution.

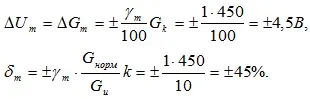
Answer. The measurement error is 45%. The voltage measured by such an error can not be considered reliable.

With limited options for choosing an instrument (voltmeter), the methodological error can be considered with the correction calculated by the formula.

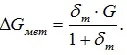
Example 1.2. Calculate the absolute error of the V7-26 voltmeter when measuring the voltage in a DC circuit. The accuracy class of the voltmeter is given by m = γ 2.5% ± maximum reduced error. The limit of the voltmeter scale used in the study is U norms \u003d 30 V.

Solution. The absolute error is calculated according to the known formulas:

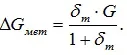
(because the reduced error, by definition, is

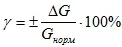
Expressed by the formula, then here you can find the absolute error:

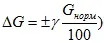
Answer. ΔU = ±0.75 V.

Important steps in the measurement process are the processing of results and rounding rules. The approximate theory of calculations, knowing the degree of accuracy of the data, allows one to assess the degree of accuracy of the results even before performing the actions:

It is enough to ensure the necessary accuracy of the result, to select data with the appropriate degree of accuracy, but not too high to save the calculator from unnecessary calculations, rationalize the calculation process, freeing it from calculations that will not affect the exact number of results.

Rounding rules are applied when the results are processed.

• Rule 1 If the first of the discarded figures is greater than five, the last of the figures kept is increased by one.

• Rule 2 If the first of the figures thrown is less than five, no increase is made.

• Rule 3 If the discarded number is five and there is no significant number behind it, rounding is made to the nearest even number. The last stored digit does not change if it is even and increases if it is not even.

If there are meaningful numbers after five, rounding is carried out according to rule 2.

We do not improve rounding accuracy by applying rule 3 to round a single number. But with multiple rounding, the extra numbers will be as common as the few numbers. Mutual error compensation will ensure the highest accuracy of the result.

A number known to be greater than (or, in the worst case, equal) the absolute error. Limiting absolute error

The value of the marginal error is not entirely certain. Its marginal error (absolute or relative) must be known for each approximate number.

When not shown directly, it becomes clear that the maximum absolute error is half of the unit of the last discharged discharge. Thus, if the number approximately 4.78 is given without specifying the marginal error, it is understood that the marginal absolute error is 0.005.

As a result of this agreement, you can always do without specifying the marginal error of a number rounded according to the rules of 1-3; that is, if the letter α denotes the approximate number, then.

When Δn is the final absolute error, and δ n is a relative limiting error.
Additionally, when processing the results, the error rules are total, Difference, Product, and Partition.

• Rule 1 The absolute limiting error of the sum is equal to the sum of the total limiting mistakes of the individual terms. Still, when there are significant errors in the words, mutual compensation for the mistakes usually occurs, so the actual error of the sum occurs only in exceptional cases. The states coincide with or are close to the limiting mistake.

• Rule 2 The absolute limiting error of the difference is equal to the sum of the negative or the total limiting errors of the output.

The relative limiting error is easy to find by calculating the absolute limiting error.

• Rule 3 The relative limiting error of the sum (but not the difference) is between the smallest and the largest of the relative errors of the terms.

If all terms have the same marginal relative error, the aggregate has the same marginal relative error. In other words, in this case, the accuracy of the sum (in percentages) is not inferior to the accuracy of the terms.

In contrast to the total, the difference between the approximate numbers can be less accurate than the minus and subtracted ones. The loss of precision is especially significant when the minus and the output differ little.

• Rule 4 The relative limiting error of the product is approximately equal to the sum of the relative limiting errors of the factors: δ \u003d δ 1 + δ 2 or more precisely, δ \u003d δ 1 + δ 2 + δ 1 δ 2 is the relative error of the product δ here is the relative error of the product, δ 1 δ 2 – are relative error factors.

Notes:

If approximate numbers with the same significant digits are multiplied, the same number of significant digits should be kept in the multiplication. The last stored figure will not be completely reliable.
If some factors have more significant digits than others, then before multiplying, the first ones should be rounded up, holding at least as many digits as the correct element has or one more (as a backup); it is useless to save other figures.
If the multiplication of two numbers is supposed to have a predetermined and completely reliable number, then in each factor, there must be one more exact number of digits (obtained by measurement or calculation). If the number of elements is more than two and less than ten, then the precise figures for a full guarantee in each factor must be two units more than the number of exact statistics required. In practice, it is pretty enough to get just one extra figure.

• Rule 5 The bounding relative error of the partition is approximately equal to the sum of the delimiter relative errors of the divider and the divisor. The exact value of the relative limiting error consistently exceeds the approximate value. The excess percentage is approximately equal to the relative limiting error of the divider.

Example 1.3. Find the absolute limiting error of section 2.81:0.571.

Solution. The marginal relative error of the dividend is 0.005:2.81=0.2; divider – 0.005: 0.571 = 0.1%; private – 0.2% + 0.1% = 0.3%. The absolute limiting error of the partition will be approximately 2.81: 0.571 0.0030 = 0.015.

This means that the third significant figure in section 2.81:0.571=4.92 needs to be more reliable.

Answer. 0,015.

Example 1.4. Assuming that the voltmeter has an infinitely large resistance and does not bring distortions to the measured circuit, calculate the relative error of the voltmeter readings connected to the course (Figure 1.3). Classify the measurement error for this task.

Pilaf. 1.3

Solution. Let us show the readings of an accurate voltmeter as I and a voltmeter with infinitely large resistance over the I ∞. Required relative error

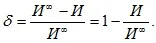
attention, that

then we get it

Since R AND >>R and R>r, the fraction in the denominator of the final equation is less than one. Therefore, we can use the approximate

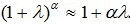
formula. It applies to λ α 1 for any ≤. Assuming that α in this formula = -1 and λ= RR (r+R) -1 R AND -1, we get δ ≈ R/(r+R) R AND.

The more excellent the voltmeter’s resistance compared to the circuit’s external resistance, the smaller the error. But the condition is R<

Answer. Error systematic and organized.

Example 1.5. The DC circuit includes the following devices (Figure 1.4): A – ammeter type M 330 with accuracy class K A \u003d 1.5, I k \u003d with a measurement limit of 20 A; A 1 – ammeter type M 366 accuracy class K A1 \u003d 1.0, with measuring limit I k1 \u003d 7,5 A. If the devices show, find the largest possible relative error in measuring the current I and the possible limits of its true value. \u003d 8 .0A. and I 1 \u003d 6.0A. Classify the measurement.

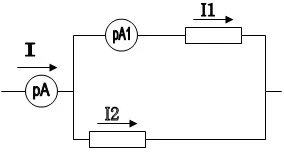
Pilaf. 1.4

Solution. We determine the current I 2 based on the device readings (excluding errors): I 2 \u003d I-I 1 \u003d 8.0-6.0 \u003d 2.0 A.

Find modules of absolute errors of ammeters A and A 1

We have

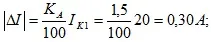
equality for Aampermeter

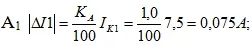
Let’s find out the sum of the modules of absolute errors:

Therefore, the largest possible and the same value expressed in fractions of this value equals 1. 10 3 – for one device; 2 10 3 – for another device. Which of these tools will be the most accurate?

Solution. The device’s accuracy is characterized by a value corresponding to the error (the more accurate the device, the smaller the error), that is. For the first device, this will be 1 / (1. 10 3) = 1000, and for the second – 1 / (2. 10 3) = 500. Notice that the > 1000 is 500. Therefore, the first device is twice as accurate as the second.

A similar conclusion can be reached by checking the appropriateness of the errors: 2 . 10 3 / 1 . 10 3 = 2.

Answer. The first device is twice as accurate as the second.

Example 1.6. Find out the sum of the approximate measurements of the device. Find the current number of characters: 0.0909 + 0.0833 + 0.0769 + 0.0714 + 0.0667 + 0.0625 + 0.0588+ 0.0556 + 0.0526.

Solution. Summing up all the measurement results, we get 0.6187. The maximum error of the sum is 0.00005 9=0.00045. This means that an error of up to 5 units is possible in the last fourth digit of the total. Therefore, we round the amount to the third decimal place, that is. one in a thousand, and we get 0.619 – a result in which all the signs are correct.

Answer. 0.619. The current number of characters is three decimal places.

.”The concept of “error accuracy characterizes physical quantities. There is a saying that you can have information by taking measurements. Thus, like any other, it will be possible to find the house’s height or the street’s length.

Introduction

Let’s understand the meaning of the concept of “measuring value.” The process of measurement is to compare homogeneous quantities taken as units.

To determine the volume, liters are used to calculate the mass. Grams are used. To make calculations more manageable, we introduced the SI system of the international classification of units.

To measure the length of the swamp in meters, mass – kilograms, volume-liters, time-seconds, and speed-meters per second.

Using the traditional method when calculating physical quantities is only sometimes necessary. It is enough to apply the calculation using a formula. To calculate average speed, you need to divide the distance traveled by the time spent on the road. This is how the average rate is calculated.

They are called multiples using units of measurement ten, hundred, and thousand times higher than the indicators of the accepted units of measurement.

The name of each prefix corresponds to its multiplier number:

1. Deca.

2. Hello.

3. Kilo.

4. Mega.

5. Giga.

6. Tera.

In physical science, a multiple of 10 is used to write such multipliers. For example, one million is shown as 106.

In a simple ruler, one unit of length measurement is one centimeter. It is 100 times smaller than one meter. A ruler of 15 cm is 0.15 m long.

A ruler is the simplest type of measuring instrument for measuring length. A thermometer represents more complex devices – a hygrometer – an ammeter for determining humidity – to measure the force at which an electric current is emitted.

How Accurate will the Measurements be?

Take a ruler and a simple pencil. Our task is to measure the length of this stationery.

First, you need to determine the division value indicated on the scale of the measuring device. Numbers are written in the two compartments that are the closest strokes of the scale, for example, “1” and “2”.

It is necessary to calculate how many divisions are put in the range of these numbers. If you count correctly, you will get “10”. Subtract from the more significant number the number that will be less, and divide by the number that forms the divisions between the digits:

(2-1)/10 = 0.1 (cm)

So we determine whether the price that determines the division of stationery is 0.1 cm or 1 mm. It is clearly shown how the price indicator for the division is determined using any measuring device.

We will use the knowledge we have acquired by measuring a pencil whose length is a little less than 10 cm. In the absence of small partitions on the ruler, it is concluded that the object’s length is 10 cm. This approximate value is called the measurement error. Indicates the level of inaccuracy that can be tolerated in the measurement.

By specifying item length parameters with a higher level of accuracy, a more significant division value provides greater measurement accuracy, which results in a minor error.

In this case, accurate measurements cannot be made. And indicators should not exceed the size of the price of the division.

It was determined that the dimensions of the measurement error were 1/2 of the price specified in the sections of the instrument used to determine the measurements.

After measuring the pencil at 9.7 cm, we determine the indicators of its error. This is a gap of 9.65 – 9.85 cm.

The formula that measures such an error is the calculation:

A = bir ± D (a)

A – in the form of a quantity for measurement processes;

a – the value of the measurement result;

D – the definition of absolute error.

When subtracting or adding incorrect values, the result will equal the sum of the error indicators, each of which is a different value.

Introduction to the Concept

If we consider it depending on the way it is expressed, we can distinguish the following varieties:

Absolute.
Consanguineous.
Given.

The absolute measurement error is indicated by the capital letter “Delta.” This concept is defined as the difference between the measured and actual values of the measured physical quantity.

The expression of absolute measurement error is units of the quantity that must be measured.

When measuring the mass, it will be expressed, for example, in kilograms. This is not a measurement accuracy standard.

How is the Error of Direct Measurements Calculated?

There are ways to show and calculate measurement errors. To do this, it is crucial to determine the physical quantity with the necessary accuracy, know the absolute measurement error, and understand that no one will ever find it. You can only calculate the limit value.

This term explicitly refers to boundary data, even if used conditionally. Absolute and relative measurement errors are indicated by the same letters; the difference is in their spelling.

When measuring length, the absolute error will be measured in the units in which the distance is calculated. And since the relative error is the ratio of absolute error to the measurement result, it is calculated without dimensions. This value is usually expressed as a percentage or fraction.

Absolute and relative measurement errors have several different calculation methods, depending on which physical quantities are.

The Concept of Direct Measurement

The absolute and relative error of direct measurements depends on the accuracy class of the instrument and its ability to determine the weighing error.

Before discussing how the error is calculated, it is necessary to clarify the definitions. Direct measurement is a measurement in which the result is read directly from the instrument scale.

When we use a thermometer, ruler, voltmeter, or ammeter, we always measure directly because we use a now-scaled device.

Two factors affect performance:

Instrument error.
An error in the reference system.

For direct measurements, the absolute error limit will equal the sum of the error indicated by the device and the error that occurs during the reading process.

D = D (pr.) + D (yok)

Example of a Medical Thermometer

Accuracy values are indicated on the device itself. An error of 0.1 degrees Celsius is recorded on a medical thermometer. The read error is half the value of the split.

D = C/2

If the division value is 0.1 degrees, then calculations for a medical thermometer can be made:

D \u003d 0.1 o C + 0.1 o C / 2 \u003d 0.15 o C

There is a technical specification on the back side of the balance of another thermometer. For accurate measurement, it is indicated that the thermometer must be immersed together with the entire rear part. Unspecified. The only error left is the counting error.

If the division value of the scale of this thermometer is 2 o C, you can measure the temperature with an accuracy of 1 o C. These are the limits of the permissible absolute measurement error and the calculation of the absolute measurement error.

A special system is used to calculate accuracy in electrical measuring devices.

Accuracy of Electrical Measuring Devices

A value called the accuracy class is used to indicate the accuracy of such devices. The letter “Gamma” is used for its definition. To accurately determine absolute and relative measurement errors, you need to know the accuracy class of the device indicated on the scale.

For example, take an ammeter. Its scale shows the accuracy class, which represents the number 0.5. Suitable for direct and alternating current measurements refers to the devices of the electromagnetic system.

This is a fairly accurate device. If you compare it with a school voltmeter, you can see that the accuracy class is 4. This value must be known for later calculations.

Application of knowledge

Thus, D c \u003d c (max) X γ / 100

This formula will be used for specific examples. Let’s use a voltmeter and find the error when measuring the voltage given off by the battery.

Let’s connect the battery directly to the voltmeter, checking whether the arrow is at zero earlier. When the device was connected, the arrow deviated from the 4.2 sections. This situation can be explained as follows:

It can be seen that the maximum U value for this element is 6.
Accuracy class -(γ) = 4.
U(o) = 4.2 V.
C=0.2V

Using this formula data, absolute and relative measurement errors are calculated as follows:

DU \u003d DU (ör.) + C / 2

YOU (pr.) \u003d U (max) X γ / 100

DU (pr.) \u003d 6 V X 4/100 \u003d 0.24 V

This is the fault of the device.

The calculation of the absolute measurement error, in this case, will be made as follows:

DU = 0.24 V + 0.1 V = 0.34 V

Using the considered formula, you can quickly learn how to calculate the absolute measurement error.

There is a rule for rounding errors. It allows you to find the average between the absolute error limit and the relative error limit.

Learn to identify a weighing Error

This is an example of direct measurements. It is weighed in a special place. After all, leveraged scales have no scales. Let’s find out how to determine the error of such an operation. The accuracy of the mass measurement is influenced by the accuracy of the weights and the perfection of the balances.

We use a scale with a set of weights that must be placed exactly on the right side of the balance. Take a ruler to weigh.

Before starting the test, you need to balance the balances. We put the ruler in the left bowl.

The mass will be equal to the sum of the installed weights. Let’s determine the measurement error of this quantity.

D m = D m (ağırlıklar) + D m (ağırlıklar)

Mass measurement error consists of two terms associated with balances and weights. To find out each of these values, products in factories for manufacturing scales and weights are supplied with special documents that allow you to calculate their accuracy.

Applying Tables

Let’s use a standard table. The fault of the balance depends on how much mass is put on the balance. The larger it is, the greater the error, respectively.

Even if you put a very light body, there will be a mistake. This is due to the friction process that occurs on the axles.

The second table concerns a set of weights. It indicates that each of them has its mass error. 10 grams has an error of 20 grams and 1 mg. We calculate the sum of the errors of each of these weights taken from the table.

It is convenient to write the mass and mass error in two lines, one after the other: the smaller the weight, the more accurate the measurement.

Results

It was found impossible to determine the absolute error during the material under consideration. You can only set limit indicators. For this, the formulas described above are used in the calculations. This material is recommended for school students in grades 8-9. Based on the information obtained, solving problems for determining absolute and relative errors are possible.

Measurements are called straight if the values of quantities are determined directly by instruments (for example, measuring length with a ruler, determining the time with a stopwatch, etc.). Measurements are called direct if the value of the measured quantity is determined by direct measurements of other amounts associated with the specific relationship measured.

Random Errors in direct Measurements

Absolute and relative error. Allow keeping measurements of the same amount in the absence of systematic error. The individual measurements look like x 1,x2, …, xn. The average value of the measured amount is best selected:

The absolute error of a single measurement is called the difference of the form:

Average absolute error single measurements:

(2)

the average absolute error sought.

The relative error is the ratio of the average absolute error to the average value of the measured quantity:

. (3)

Device errors in direct measurements

If there are no special instructions, the error of the device is equal to half the value of the division (ruler, beaker).
The error of tools equipped with bolts is equal to the division value of the sliding (micrometer – 0.01 mm, caliper – 0.1 mm).
The error of the table values is equal to half of the unit of the last digit (five units of the sequence after the last significant digit).
The error of electrical measuring devices is calculated based on the accuracy class. SPECIFIED ON THE THE INSTRUMENT SCALE FROM:

For example:

Where you are the maximum, and I am the maximum – the measurement limit of the device.

The error of devices with a digital indicator is equal to the unit of the last digit of the indicator.

After evaluating random and instrumental errors, the one with a large value is considered.

Calculation of errors in indirect measurements

Most measurements are indirect. In this case, the desired value X is a function of several variables. A,b,c…, the values of which can be found by direct measurements: Х = f(a,b,c…).

The arithmetic mean of the result of indirect measurements will be equal to the following:

X = f( a, b, c…).

One of the ways to calculate the error is to differentiate the natural logarithm of the function X = f(. a,b,c…). For example, if the relation X = determines the desired value of X, then after getting the logarithm, we get an X = lna+lnb+ln(c+d).

The differential of this statement:

About the calculation of approximate values, the relative error it can be written as follows:

 =

. (4)

The absolute error, in this case, is calculated by the following formula:

X = X(5)

Thus, the calculation of errors and the calculation of the result for indirect measurements are carried out in the following sequence:

1) Make measurements of all quantities in the original formula to calculate the final result.

2) Calculate the arithmetic mean values of each measured value and their absolute errors.

3) In the original formula, change the average values of all measured values, and calculate the average value of the desired value:

X = f( a, b, c…).

4) Get the logarithm of the original formula X = f(a,b,c…) and write down the expression of the relative error in formula (4) format.